Jerk-Limited Trajectory

This post tries to explain the basics of a trajectory that tries to limit the acceleration or the jerk. If you are not familiar, the jerk is the first time derivative of the acceleration.

Basic Example

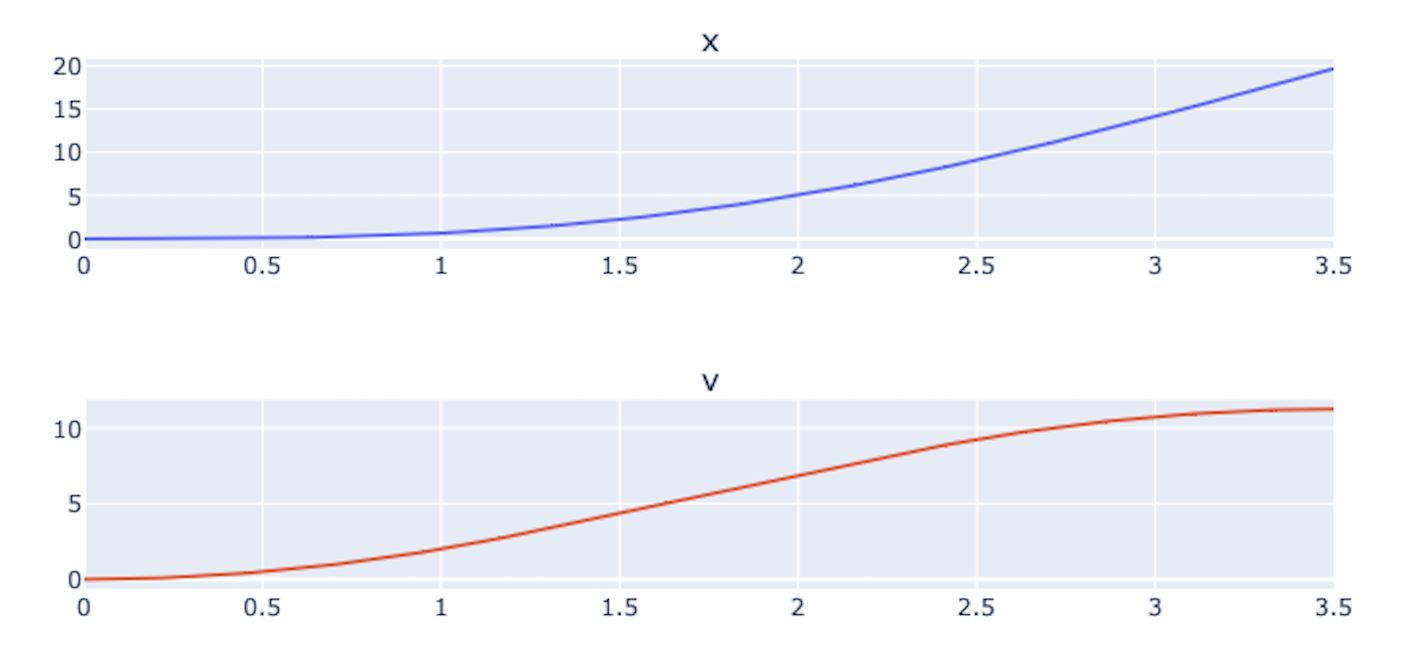
This plot shows the position, velocity, acceleration, and jerk as a function of time for a 1-dimensional jerk-limited trajectory starting with all zero, except a positive jerk of 4 m/s^3. Then it reaches a maximum acceleration limit of 5 m/s^2, and stays there for a second. After that, the a negative jerk of 4 m/s^3 is applied until the acceleration is reached 0 m/s^2.

In other words, the object starts stationary, and reaches a constant velocity of 11.25 m/s, in a jerk-limited fashion.

Extended Example

The navigation of a robot can be complex. Even for the simple trajectories, user may need to determine the path the robot would take as a function of time. The objective of the waypoint-based navigation generation algorithms is to simplify this.

Here, the user defines a set of key navigation points that the system needs to through. These are referred to as the waypoints. These do not necessarily has to be strictly position-based waypoints, and may include other kinematic states such as velocity or acceleration. Then, a trajectory generation algorithm creates an optimal smooth curve that goes through all these waypoints.

Acceleration-Limited Trajectory Example

One method of this waypoint generation is to consider the second-order constraints of the dynamic systems: velocity and acceleration. These assume that the acceleration can be controlled arbitrarily to a maximum/minimum limit. Changing the acceleration eventually controls the velocity and the position of the robotics system. This can be referred to as the acceleration-limited trajectory generation. One drawback of using this method the need to change the acceleration abruptly.

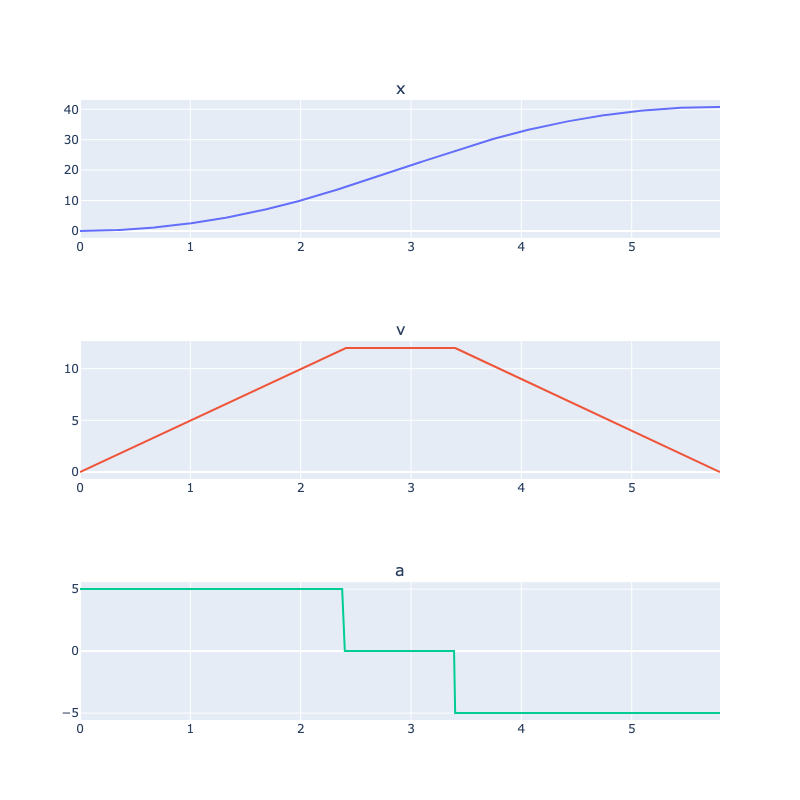
Jerk-Limited Trajectory Example

Another common method of waypoint generation is to consider the third-order constraints of the system dynamics. Here, all of velocity, acceleration, and jerk (the first derivative of acceleration) are taken into account. It is assumed that the jerk can be controlled arbitrarily up to some limit. This generates a smoother trajectory provides without abrupt changes acceleration or velocity, which reduces wear and tear, and the mechanical stress of the system. As such, jerk-limited trajectories are commonly used in practical robotic systems.

This example shows a jerk-limited trajectory for an object that reaches a constant velocity of 11.25 m/s. Note that the second waypoint is a velocity waypoint that does not include position requirements.

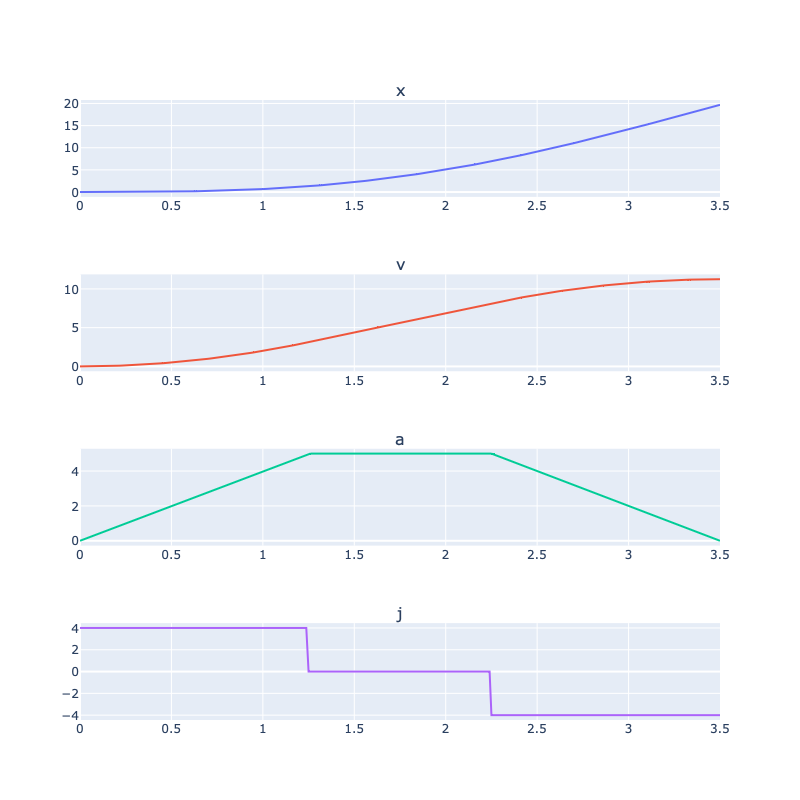
This plot shows the position, velocity, acceleration, and jerk as a function of time for a 1-dimensional jerk-limited trajectory starting with all zero, except a positive jerk of 4 m/s^3. Then it reaches a maximum acceleration limit of 5 m/s^2, and stays there for a second. After that, the a negative jerk of 4 m/s^3 is applied until the acceleration is reached 0 m/s^2.